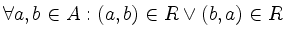Mathe n-stelliges Kreuzprodukt

[Seth93]

Hallo,

wie sieht ein n-stelliges Kreuzprodukt aus?
AxBXC = {(a1,b1,c1)...}
oder AxBxC = {((a1,b1),c1)...}

 

[DaPhreak]

wie sieht ein n-stelliges Kreuzprodukt aus?
AxBXC = {(a1,b1,c1)...}
oder AxBxC = {((a1,b1),c1)...}

Ich verstehe die Frage nicht. Was meinst Du mit "n-stelliges Kreuzprodukt", das Kreuzprodukt aus n Vektoren der Länge drei? Das Kreuzprodukt aus Vektoren der Länge n?

Was bedeutet AxBxC, sind A, B, C Vektoren und es geht um das Kreuzprodukt aus allein dreien? Falls das so ist, also A = [a1;a2;a3], B = [b1;b2;b3] und C = [c1;c2;c3], dann ist noch zu beachten, dass das Kreuzprodukt nicht assoziativ ist. So ist (A x B) x C gleich dem Dreiervektor hier:

 - c2*(a1*b2 - a2*b1) - c3*(a1*b3 - a3*b1)
   c1*(a1*b2 - a2*b1) - c3*(a2*b3 - a3*b2)
   c1*(a1*b3 - a3*b1) + c2*(a2*b3 - a3*b2)

... während A x (B x C) so aussieht:

   a2*(b1*c2 - b2*c1) + a3*(b1*c3 - b3*c1)
   a3*(b2*c3 - b3*c2) - a1*(b1*c2 - b2*c1)
 - a1*(b1*c3 - b3*c1) - a2*(b2*c3 - b3*c2)

Ansonsten verstehe ich leider auch nicht was die geschweiften und die runden (insbesondere die verschachtelten runden) Klammern bedeuten.


Falls Du wirklich auf Vektoren der Länge n abzielst dann schau mal hier.

 

[Seth93]

Ich bin bei Mengen und nicht bei Vektoren ^^
Ich weiß nicht, ob es da einen Unterschied gibt, aber dem scheint so.

Vielleicht kennst du das Kreuzprodukt auch unter dem Wort "kartesisches Produkt".

 

[DaPhreak]

Ah okay, da war ich auf dem falschen Dampfer. Kannte das wirklich nur als kartesisches Produkt.

In dem Fall: Ich kenne die Definition so: A x B ist eine Menge von Tupeln (an,bm) wobei an und bm alle Elemente der Mengen A und B sind. Wendet man die Definition streng an, dann ist

(A x B) x C = {((a1,b1),c1), ((a2,b2),c2), ...}
A x (B x C) = {(a1,(b1,c1)), (a2,(b2,c2)), ...},

das Kreuzprodukt ist also eigentlich nicht assoziativ. Natürlich ließen sich beide Mengen da oben sehr einfach bijektiv auf die Menge

{(a1,b1,c1),(a2,b2,c2),...}

abbilden. Und ich glaube auch durchaus, dass diese häufig gebraucht und verwendet wird. Insofern wäre es sinnvoll, sich dafür eine Notation zu definieren. Gerade wenn keine Klammern angegeben sind, also einfach A x B x C könnte man das Ergebnis davon so definieren. Ich weiß allerdings nicht inwiefern das üblich ist.


Gesehen habe ich jedenfalls schon oft Dinge àla A x A x ... x A = A[sup]n[/sup] was einfach als n-Tupel aller Elemente aus n verstanden wird. Beispiel {0,1}[sup]n[/sup] = Menge aller n-stelligen Binärzahlen.

 

[Seth93]

Ok, das kam auch gestern in den Übungen dran
Vielen Dank.

Kennst du dich auch noch mit Äquivalenzrelationen aus?
Die Frage lautet: Welche der folgenden Relationen ist eine Äquivalenzrelation?

„x und y sind ungerade“ auf der Menge N>=1

Antwort:
keine Äquivalenzrelation (die Relation ist nicht reflexiv – beispielsweise steht 3 nicht mit sich selbst in Relation)

https://de.wikibooks.org/wiki/Mathe_für_Nicht-Freaks:_Relation:_Äquivalenzrelation

Aber wieso ist sie nicht reflexiv?
Was spricht denn gegen (3,3)?



EDIT:
Gilt eigt für eine Menge x Menge immer, dass sie auch eine Äquivalenzrelation ist?
M = {1,2}
M^2 = {(1,1), (1,2), (2,1), (2,2)}

Wie sieht es mit M = {1} aus?
Reflexiv und symmetrisch ist sie, aber was ist mit transitiv?

 

[DaPhreak]

Die Frage lautet: Welche der folgenden Relationen ist eine Äquivalenzrelation?

„x und y sind ungerade“ auf der Menge N>=1

Antwort:
keine Äquivalenzrelation (die Relation ist nicht reflexiv – beispielsweise steht 3 nicht mit sich selbst in Relation)

Sicher, dass das die Aufgabe war? Restklassen sind eigentlich das klassische Beispiel für Äquivalenzrelationen und was Du da stehen hast ist eine Restklasse (modulo 2).

Anders ist es wenn man nach der Relation "|x-y| ist ungerade" fragt, die ist nämlich in der Tat nicht reflexiv (Beispiel 3).

EDIT:
Gilt eigt für eine Menge x Menge immer, dass sie auch eine Äquivalenzrelation ist?
M = {1,2}
M^2 = {(1,1), (1,2), (2,1), (2,2)}

Ich denke schon, ja. Jede Äquivalenzrelation ist die Teilmenge des kartesischen Produktes der Ursprungsmenge und wenn man das volle kartesische Produkt betrachtet, dürfte reflexiv, transitiv und symmetrisch hinhauen.

Wie sieht es mit M = {1} aus?
Reflexiv und symmetrisch ist sie, aber was ist mit transitiv?

Ja, ist auch transitiv. Stur die Definition anwenden, das funktioniert.

 

[Seth93]

Alles klar. Vielen Dank!

Was sind totale Relationen?
total, wenn je zwei Elemente in mindestens einer Richtung in Relation stehen:

Wenn ich eine Relation mit 3 Elementen habe. Wie muss dann die Relation dazu aussehen?

 

[DaPhreak]

Wenn ich eine Relation mit 3 Elementen habe. Wie muss dann die Relation dazu aussehen?

Denkbar wäre eine Erweiterung àla für alle a, b, c Є A:

(a,b,c) Є R v (a,c,b) Є R v (b,a,c) Є R v (b,c,a) Є R v (c,a,b) Є R v (c,b,a) Є R

ob das aber sinnvoll ist, weiß ich nicht. Ich habe es jedenfalls noch nie gesehen, kenne Eigenschaften wie diese nur in Verbindung mit binären Relationen.

 

[Seth93]

Hi,

sry ich habe mich falsch ausgedrückt.
Ich meine, was ist wenn die Menge 3 Elemente hat?
Mein Problem ist zurzeit, dass ich total nicht verstehe.
Ich verstehe linkstotal, rechtstotal, aber total nicht.

Angenommen wir haben eine Menge M = {1,2,3,4}.
Jetzt bilden wir daraus eine Relation R = MxM. Wie sehe die totale Eigenschaft aus?

 

[DaPhreak]

Angenommen wir haben eine Menge M = {1,2,3,4}.
Jetzt bilden wir daraus eine Relation R = MxM. Wie sehe die totale Eigenschaft aus?

Für jedes Tupel (a,b) was Du in M bilden kannst muss entweder (a,b) oder (b,a) in R sein. Dabei ist das oder kein exklusives, es dürfen auch (a,b) und (b,a) in R sein.

An Deinem Beispiel: (1,2) oder (2,1) muss drin sein; (1,3) oder (3,1) muss drin sein; (1,4) oder (4,1) muss drin sein; (2,3) oder (3,2) muss drin sein; usw.

Total wäre diese hier: {(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)}
aber auch diese hier: {(1,2),(3,1),(1,4),(3,2),(4,3),(2,4)}
darf natürlich auch mehr vorkommen, das geht auch: {(2,1),(1,2),(3,1),(1,4),(4,1),(3,2),(4,3),(2,4),(4,2)}
die hier ist aber nicht total: {(2,1),(1,4),(4,1),(3,2),(4,3),(2,4),(4,2)},
denn für a=1, b=3 ist weder (1,3) noch (3,1) drin.


Anschaulich: wann immer ich zwei Elemente der Menge nehme muss mir die Relation eine Aussage liefern der Form aRb oder bRa. Beispielsweise ist das bei Ordnungsrelationen so: bei einer totalen Ordnung kann ich immer entscheiden ob a≤b oder b≤a ist. Wäre weder (a,b) noch (b,a) in der Ordnungsrelation könnte ich die beiden nicht sortieren.