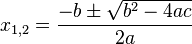[Mathe]Quatratische Funktionen

M

MinkyMausy

IT-Systemkauffrau
1 Mai 2006
311
12
Hallo Zusammen,
noch eine feine kleine Aufgabe zum späten Abend.
Diese Aufgabe haben wir heute in Lerngruppen versucht zu Lösen, nach vollen 5 (!) Stunden haben wir aufgeben.

Bitte einen genauen Lösungsweg angeben, wir vermuten stark das so eine Aufgabe in der Klausur am Montag vorkommt, sollte also leicht verständlich sein.

Danke euch!

Aufgabe:

Gegeben sei die Parabel 3x²-5x-2

a)Bestimmen Sie die Gleichung der Tangente an p (p soll die Parabel sein, also vertehen wir das so das de Tangente die Parabel schneidet)in PH (keine ahnung was PH bedeutet) P (3/10)

Soweit schon dazu rausgefunden:
-> keine Ableitung erlaubt (geht bei Aufgabe b) dann eh nicht mehr)
-> es hat irgendetwas mit der Mitternachsformel zu tun
--> -p/2 +- Wurzel (p/2)² -q Wurzel Ende
-> Steigung unbekannt

b) Von Punkt Q (2/-3) aus sollen die Tangenten an p gelegt werden. Berechnen Sie die Gleichungen der Berürungspunkte.

-> Laut Formulierung sieht es aus als wären es 2 Tangenten.
-> Man weiß ja nicht ob die Tangenten von links oder rechts kommen.


Lösungen schon vorgegeben:
a) [T:y=13x-29]
b) B1 (3/10) t1: y=13x-29
B2 (1/-4) t2: y=x-5
 
MinkyMausy schrieb:
Gegeben sei die Parabel 3x²-5x-2

a)Bestimmen Sie die Gleichung der Tangente an p (p soll die Parabel sein, also vertehen wir das so das de Tangente die Parabel schneidet)in PH (keine ahnung was PH bedeutet) P (3/10)

Soweit schon dazu rausgefunden:
-> keine Ableitung erlaubt (geht bei Aufgabe b) dann eh nicht mehr)
-> es hat irgendetwas mit der Mitternachsformel zu tun
--> -p/2 +- Wurzel (p/2)² -q Wurzel Ende
-> Steigung unbekannt
Zum Vergrößern anklicken....
Warum keine Ableitung erlaubt?
Eigentlich muss man in dem Fall nur die steigung an dem Punkt bestimmen:
f'(x)=6x-5
f'(x)=6*3-5=13

das dann in y=mx+c --> y=13x+c
um das c rauszufinden, den punkt einzetzen:
10 = 13*3+c
c = -29

--> y=13x-29


b) Von Punkt Q (2/-3) aus sollen die Tangenten an p gelegt werden. Berechnen Sie die Gleichungen der Berürungspunkte.

-> Laut Formulierung sieht es aus als wären es 2 Tangenten.
-> Man weiß ja nicht ob die Tangenten von links oder rechts kommen.
Zum Vergrößern anklicken....


das würd ich so verstehen, da Q nicht auf der Parabel liegt.
Da muss ich noch n Moment drüber nachdenken, das is mir so auf Anhieb grad nich ganz klar, wie das geht :) Antwort kommt dann hoffentlich bald :D

Lösungen schon vorgegeben:
a) [T:y=13x-29]
b) B1 (3/10) t1: y=13x-29
B2 (1/-4) t2: y=x-5
Zum Vergrößern anklicken....
 
Also bei der ersten kann ich mit der Aufgabenstellung nichts anfangen, dazu müsste man wissen, was PH ist.

Zur Zweiten:
MinkyMausy schrieb:
b) Von Punkt Q (2/-3) aus sollen die Tangenten an p gelegt werden. Berechnen Sie die Gleichungen der Berürungspunkte.
Zum Vergrößern anklicken....

Also, der Anstieg der Tangente entspricht dem Anstieg der Parabel in dem Punkt.

Den Anstieg der Tangente kann man berechnen und zwar über den Differenzenquotienten: (f(x) - (-3))/ (x-2)

Naja und jetzt gleichsetzen: f'(x) = (f(x) - (-3))/ (x-2)

HTH
 
Danke für eure Antworten, aber leider kann ich noch nichts damit anfangen, da es mit der Ableitung gemacht wurde.
Offiziell hatten wir Ableitung noch nicht, also in der Arbeit nicht erlaubt.
Diese Ableitung hat uns nur jemand erklärt weil er auch keinen anderen Weg wusste.

Laut Tipp vom Leherer Mitternachstformel.

Sorry an dieser Stelle aber dieser besagte Lehrer ist so ein A***, das er uns Aufgaben gibt die nie im Unterricht behandelt wurden und als Hausaufgabe gleich sitzen müssen und am nächsten Tag werden die HA dann als neue Thematik besprochen, aber man wird schief angesehn wenns nich richtig war.

So auch mit dieser, aufgegeben aber nie besprochen. Problem dabei, Montag Arbeit und keine Mathestunde mehr, aber Thema kommt dran.

Für weitere alternative Lösungen wär ich dankbar!!!
 
Hallo MinkyMausy,

dann versuch ich mal mein Glück...
MinkyMausy schrieb:
Gegeben sei die Parabel 3x²-5x-2

a)Bestimmen Sie die Gleichung der Tangente an p (p soll die Parabel sein, also vertehen wir das so das de Tangente die Parabel schneidet)in PH (keine ahnung was PH bedeutet) P (3/10)

Soweit schon dazu rausgefunden:
-> keine Ableitung erlaubt (geht bei Aufgabe b) dann eh nicht mehr)
-> es hat irgendetwas mit der Mitternachsformel zu tun
--> -p/2 +- Wurzel (p/2)² -q Wurzel Ende
-> Steigung unbekannt
Zum Vergrößern anklicken....

Also erstmal PH hört sich für mich an, wie Schnittpunkte mit der horizontalen Koordinatenachse (x-Achse), das würde auch erklären, wozu ihr die "Mitternachtsformel" (geiler Name) verwenden sollt, nämlich zur Bestimmung der Nullstellen der Funktion.

Deine Gleichung lautet im Allgemeinen Fall ja:
ax^2 + bx + c = f(x)

Für die "Mitternachtsformel" brauchst du aber eine Gleichung der Form:
x^2 + px + q = f(x)

Das bewerkstelligst du einfach, indem du die gesamte Gleichung durch 3 teilst, dann ist p=(-5/3) und q=(-2/3), die schmeißt du in die "Mitternachtsformel" und bekommst 2 Nullstellen raus.
x(1/2) = -(p/2) +/- sqrt((p/2)^2 - q) (sqrt() ist die Wurzel ;))

Dann haben wir jetzt alle benötigten x-Werte, juhu, und nun die "verbotene" Ableitung. Also meines Erachtens benötigt man normalerweise in jedem Fall eine Ableitung um den Anstieg exakt zu bestimmen, aber versuchen wir uns einzubilden, wir wüssten nicht, was die Ableitung ist:

Fragen wir uns, was ist der Anstieg?
Das ist die Änderung der Höhe y auf einer bestimmten Länge x, denken wir an den Straßenverkehr, die Anstiegsschilder, oder ein Anstiegsdreieck. In mathematischen Förmelchen ausgedrückt:

(f(b)-f(a))/(b-a), (b > a) oder meines Erachtens schöner:
(f(x+h)-f(x))/h

Jetzt gibts 2 Möglichkeiten:
  1. Nimm dir die zu betrachtenden Stellen x, berechne den Funktionswert für x und x+h, setze die in die Formel ein und voila, zwar nicht ganz genau, aber du hast den ungefähren Anstieg der Tangente.

    Beispiel: P=(3,10), x=3, nimm z.B. h=0.01 => x+h = 3.01 => f(x+h)=10,1303
    => (10,1303-10)/0.01 = 13,03 entspricht ganz grob deinem Anstieg an der Stelle x=3. Das setzt du für m ein, und berechnest c wie im Beispiel von chaosplanet. Je kleiner du das h wählst desto näher kommst du an die exakte Lösung.
  2. Ihr dürft den "Limes" (Grenzwert) verwenden, dann setzt du die gesamte Gleichung in die Formel und berechnest auf die Art und Weise die Ableitung, Beispiel:
    lim(h->0) (3(x+h)^2-5(x+h)-2) - (3x^2-5x-2))/h = f'(x)
    => (nach bissl rumrechnen) (3h^2 -5h+6xh)/h
    => (da kannst du h ausklammern und kürzen) => (3h-5+6x)
    => für h gegen 0, konvergiert die Gleichung gegen: 6x-5
    => also ist deine Ableitung f'(x)=6x-5, hergeleitet mit Nachdenken

Die zweite Aufgabe hat sich mir bis jetzt noch nicht vollkommen erschlossen,
unbedingt Nachfragen, falls etwas unklar ist/war.

Viele Grüße,
serialize
 
Du hast jetzt aber die p,q-Formel benutzt, das ist nicht die Mitternachtsformel. Die Mitternachtsformel ist die a,b.,c-Formel, wenn ich das noch richtig in Erinnerung hab.
 
losomat schrieb:
Du hast jetzt aber die p,q-Formel benutzt, das ist nicht die Mitternachtsformel. Die Mitternachtsformel ist die a,b.,c-Formel, wenn ich das noch richtig in Erinnerung hab.
Zum Vergrößern anklicken....

Mir ist keine der beiden Formeln als "Mitternachtsformel" bekannt, sind für mich beides Lösungsformeln. Hab diese genommen, weil MinkyMausy die ja selber schon in ihrem Text so erwähnt hat.

Warum eigentlich "Mitternachtsformel" ???
 
chaosplanet schrieb:
Uns wurde immer gesagt, dass wenn man uns um Mitternacht weckt, wir die sofort aufsagen können müssen. daher :)

Ja, das warn noch zeiten, als man um die Zeit geschlafen hat...
Zum Vergrößern anklicken....

Ahhh, danke, das erklärt einiges, dann ist es aber die mit p und q, die andere kann ich nämlich nicht aus dem Kopf, weil das Umformen ja recht einfach is...
 
serialize schrieb:
Ahhh, danke, das erklärt einiges, dann ist es aber die mit p und q, die andere kann ich nämlich nicht aus dem Kopf, weil das Umformen ja recht einfach is...
Zum Vergrößern anklicken....

ne, die pq-formel ham wir nie gehabt, und als mitternachtsformel läuft die hier:

wikipedia schrieb:
0f16872ccd04ca7ecce3544bc3521ff1.png
(a-b-c-Formel oder Mitternachtsformel)
Zum Vergrößern anklicken....
 
Also die Mitternachtsformel ist die p,q Formel, die andere kenn ich garnicht.

Wie chaosplanet es schon sagte, man sollte die zu jeder Tag und Nachtzeit aufsagegn können ;-).

Danke euch für die Antworten, heute bereit ich mich auf die Arbeit vor, da kommen sicher noch Fragen. ;)
 
Du musst dich einloggen oder registrieren, um hier zu antworten.
Zurück
Oben