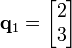Mathe Bsp bzgl. Matrix, Eigenwert, Eigenvektor

[cashgnm]

Folgendes Bsp.:

Eine symmetrische 2x2-Matrix A habe den Eigenvektor [2 3] (untereinanderstehend) zum Eigenwert λ1=-4. Finden Sie bitte einen Eigenvektor zum anderen Eigenwert λ2 von A.


Ich hab einiges herumprobiert, doch wie ich nun wirklich auf die Lösung komm, weiß ich nicht wirklich.
Habe versucht die Matrix A auszurechnen, habs dann aber nicht geschafft.
Mein Ansatz war:

A*x=λ*x
Da die Matrix symmetrisch ist, kann ich ansetzen α12=α21. d.h. wenn ich mit den gegebenen Werten in die obere Formel einsetze, kann ich die Matrix A durch die Werte α22 ausdrücken.


Wäre dann bei mir:

A= (5+2,25α22 -6-1,5α22)
(-6-1,5α22 α22)


Nur kann ich damit auch nicht wirklich etwas anfangen.

Kann mir jemand behilflich sein?

lg

 

[DaPhreak]

*edit* Ahhh, jetzt ist mir die elegante Methode aufgefallen (siehe unten).


Brechstangenmethode


Eine 2x2 symmetrische Matrix hat drei Parameter, vollkommen richtig. Kann man beispielsweise darstellen als

Die Bedingung an den Eigenvektor liefert Dir zwei lineare Gleichungen, so dass Du von 3 auf 1 Parameter reduzieren kannst, so wie Du das ja auch gemacht hast. Beispielsweise hängt also die Matrix noch von c ab.

Nehmen wir also mal an, Du hast Dich bis hierher nicht verrechnet. Dann mach doch einfach weiter.

Nächster Schritt wäre doch, den zweiten Eigenwert auszurechnen, also

anzusetzen. Das liefert Dir eine quadratische Gleichung in ?, die Du nach ? lösen kannst, die Lösungen hängen dann halt noch von c ab. Eine müsste ja nachwievor -4 sein, die zweite ist jetzt interessant.

Die nimmst Du und rechnest dann den dazugehörigen Eigenvektor aus. Wie immer:

ansetzen und nichttriviale Lösungen in q suchen. Wenn Du alles richtig machst, sollte an dieser Stelle die Abhängigkeit von c verschwinden...



Das ist natürlich mehr so die Brechstangen-Methode, die auf jeden Fall gehen sollte aber ziemlich viel Rechenwust bedeutet. Ich nehme an es gibt eine elegantere Lösung, aber die habe ich jetzt auch noch nicht entdeckt.


Ich habs mal versucht und bin auf

gekommen, aber darauf gebe ich jetzt keinerlei Gewähr...


elegantere Methode

Man kann zeigen, dass für eine reelle symmetrische Matrix die Eigenvektoren zueinander orthogonal sind. Weiß nicht ob das bei Euch schon konkret dran kam.

Läuft darauf hinaus, dass man die Eigenwertzerlegung in Matrix-Form aufschreibt:

dann das ganze transponiert und dann

mit

vergleicht. Dann kommt man drauf, dass Q eine orthogonale Matrix ist, also zwei zueinander orthogonale Spalten hat.

Folglich musst Du nur einen Vektor finden, der zu dem gegebenen

orthogonal ist. Und das ist ja nicht so schwer....

 

[cashgnm]

Vielen Dank dir schonmal

ich komm jetzt also auf

2b1=-3b2

also b1=-3/2 b2

D.h. ich kann auf jeden fall Mal den Vektorraum anschreiben, indem ich b2=β setze

Also V(λ2)={β * (-1,5 / 1) ; β E R )

d.h. b= (-1,5/1) ? Ist es egal, ob ich b=(-1,5/1) oder b=(-3/2) setze?

Und würde man nicht auch sagen können b=(3/-2) bzw. b=(1,5/-1) ?

Gibts da nun eine eindeutige Lösung für b? Und kann ich das prinzipiell gleich aus b1=-3/2b2 so setzen?

 

[DaPhreak]

Die Definitionsgleichung für einen Eigenvektor lautet ja:

Angenommen

ist einer. Dann sieht man schnell, dass auch

einer ist für ein beliebiges

. Einfach mal da oben einsetzen, das c kürzt sich raus.

In anderen Worten: Der Eigenvektor ist nur in seiner Richtung eindeutig bestimmt, nicht aber in seiner Länge. Jede beliebig skalierte Version des Eigenvektors ist richtig. Manche normieren ihn künstlich auf Länge 1, aber das ist auch nicht unbedingt schöner. Um die Lösung anzugeben wählt man halt einfach einen aus, der sich schön aufschreiben lässt.